用 JavaScript 写出一个彩票系统?
用 JavaScript 写出一个彩票系统?
原本这篇文章是打算叫「假如我是彩票系统开发者」,但细想一下,如果在文章中引用太多的 JavaScript 的话,反而不是那么纯粹,毕竟也只是我的一厢情愿,彩票开发也不全如本文所讲,有所误导的话便也是得不偿失了。
所以索性就叫「用 JavaScript 写出一个彩票系统」,也算明朗了一些,声明一下,真实的彩票系统不是这么开发出来的,也不具备明面上的规律,我们应该相信彩票的公正性,尽管其可能不是基于随机!
# 杂谈
最近大抵是迷上彩票了,幻想着自己若能暴富,也可以带着家庭 "鸡犬升天" 了,不过事与愿违,我并没有冲天的气运,踏踏实实工作才是出路?
买彩票的时候,我也考虑了很久,到底怎么样的号码可以在 1700 万注中脱颖而出,随机试过,精心挑选的也试过,找规律的模式也试过,甚至我还用到了爬虫去统计数据,啼笑人非!
我们默认彩票系统是基于统计学来实现一等奖的开奖,那么历史以来的一等奖理所当然应该是当期统计率最低的一注,所以,最开始的时候我是这么想的:
- 获取历史以来所有的中奖彩票号码
- 使用代码去统计出所有号码的中奖次数
- 按照出现几率最低的数字来排序
- 依次组成某几注新号码
天马行空,却也是自己发财欲望的一种发泄渠道罢了,称之为异想天开也不为过,扯了挺多,哈哈!
上面的思路我已经实践过了,用了差不多一年的时间,没有用!别用!当然你也可以试试,如果你中了,恭喜,你才是天选之人!
# 彩票的规则
我们这里的彩票规则统一使用「双色球」的规则来说明,其购买的规则如下:
- 红球为六位,选项从 1 - 33 中挑选,不可重复
- 蓝球为一位,选项从 1 - 16 中挑选
- 红蓝双色球一共七位组成一注
一等奖一般中全部购买的注里面挑选一注,这一注可能被多个人买,也有可能是一个人买了该注的倍数。
所以粗略统计,彩票的中奖几率计算公式如下所示:
使用组合数公式来计算,从 n 个元素中取 k 个元素的的组合数公式为:
根据公式,我们可以很容易的写出来一个简单的算法:
function factorial(n) {
if (n === 0 || n === 1) {
return 1
} else {
return n * factorial(n - 1)
}
}
function combination(n, k) {
return factorial(n) / (factorial(k) * factorial(n - k))
}
console.log(combination(33, 6) * combination(16, 1)) // 17721088
2
3
4
5
6
7
8
9
10
11
12
13
所以可以得出的结论是,双色球头奖的中奖几率为:
# 数据量
我们通过上面的算法得知了彩票的总注数为 17721088 ,那么这么多注数字组成的数据到底有多大呢?
简单计算下,一注彩票可以用 14 个数字来表示,如 01020304050607 ,那么在操作系统中,这串数字的大小为 14B ,那么粗略可知的是,如果所有的彩票注数都在一个文件中,那么这个文件的大小为:
const totalSize = 17721088 * 14 / 1024 / 1024 // 236.60205078125MB
很恐怖的数量,有没有可能更小?我们研究一下压缩算法!
01 这个数字在内存中的占用是两个字节,也就是 2B,那如果我们把 01 用小写 a 代替,那么其容量就可以变成 1B,总体容量可减少一半左右!

这样子的话,我们上面的一注特别牛的号码 01020304050607 就可以表示为 abcdefg !
这就是压缩算法最最最基本的原理,压缩算法有很多种,大体分为有损压缩和无损压缩,对于我们数据类的内容来讲,我们一般都会选择无损压缩!
- 有损压缩算法:这些算法能够在压缩数据时丢弃一些信息,但通常能在不影响实际使用的前提下实现更高的压缩比率,其中最常见的是图像、音频和视频压缩算法
- 无损压缩算法:这些算法不会丢弃任何信息,它们通过查找输入数据中的重复模式,并使用更短的符号来表示它们来实现压缩。无损压缩算法常用于文本、代码、配置文件等类型的数据
首先,让我们先准备一些测试数据,我们使用下面这个简单的组合数生成算法来获取出 1000 个组合数:
function generateCombinations(arr, len, maxCount) {
let result = []
function generate(current, start) {
// 如果已经生成的组合数量达到了最大数量,则停止生成
if (result.length === maxCount) {
return
}
// 如果当前已经生成的组合长度等于指定长度,则表示已经生成了一种组合
if (current.length === len) {
result.push(current)
return
}
for (let i = start; i < arr.length; i++) {
current.push(arr[i])
generate([...current], i + 1)
current.pop()
}
}
generate([], 0)
return result
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
接下来,我们需要生成 1000 注双色球,红球是从 1 - 33 中取组合数,蓝球是从 1 - 16 中依次取数
function getDoubleColorBall(count) {
// 红球数组:['01', '02' .... '33']
const arrRed = Array.from({ length: 33 }, (_, index) => (index + 1).toString().padStart(2, '0'))
const arrRedResult = generateCombinations(arrRed, 6, count)
const result = []
let blue = 1
arrRedResult.forEach(line => {
result.push(line.join('') + (blue++).toString().padStart(2, '0'))
if (blue > 16) {
blue = 1
}
})
return result
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
我们将获取的彩票内容放在文件中以便于下一步操作:
const firstPrize = getDoubleColorBall(1000).join('')
fs.writeFileSync('./hello.txt', firstPrize)
2
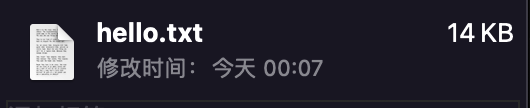
这样子,我们就得到了第一版的文件,这是其文件大小:
试一下我们初步的压缩算法,我们将刚刚设定好的规则,也就是数字到字母的替换,用 JavaScript 实现出来,如下:
function compressHello() {
const letters = 'abcdefghijklmnopqrstuvwxyzABCDEFG'
const doubleColorBallStr = getDoubleColorBall(1000).join('')
let resultStr = ''
for (let i = 0; i < doubleColorBallStr.length; i+=2) {
const number = doubleColorBallStr[i] + doubleColorBallStr[i+1]
resultStr += letters[parseInt(number) - 1]
}
return resultStr
}
const firstPrize = compressHello()
fs.writeFileSync('./hello-1.txt', firstPrize)
2
3
4
5
6
7
8
9
10
11
12
13
这样我们就得到了一个全新的 hello 文件,他的大小如下所示,正好印证了我们的想法!

如果按照这个算法的方法,我们能将之前的文件压缩至一半大小,也就是 118.301025390625MB ,但是这就是极限了吗?不,上面我们讲过,这只是最基本的压缩,接下来,让我们试试更精妙的方法!
# 更精妙的方法
这里我们不对压缩算法的原理做过多的解释,如果诸位感兴趣的话,可以自己寻找类似的文章阅读,鉴于网上的文章质量参差不齐,我就不做推荐了!
这里我们需要了解的是,我们正在研究的是一个彩票系统,所以他的数据压缩应该具备以下几个特征:
- 具备数据不丢失的特性,也就是无损压缩
- 压缩率尽可能小,因为传输的文件可能非常大,如我们上面举的例子
- 便于信息的传输,也就是支持 HTTP 请求
常做前端的同学应该知道,我们在 HTTP 请求头里面常见的一个参数 content-encoding: gzip ,在项目的优化方面,也会选择将资源文件转换为 gzip 来进行分发。在日常的使用中,我们也时常依赖 Webpack , Rollup 等库,或者通过网络服务器如 nginx 来完成资源压缩, gzip 不仅可以使得发送的内容大大减少,而且客户端可以无损解压访问源文件。
那么,我们能不能使用 gzip 来完成压缩呢?答案是可以, Node.js 为我们提供了 zlib 工具库,提供了相应的压缩函数:
const zlib = require('zlib')
const firstPrize = compressHello()
fs.writeFileSync('./hello-2.txt.gz', zlib.gzipSync(firstPrize))
2
3
4
得到的结果是:
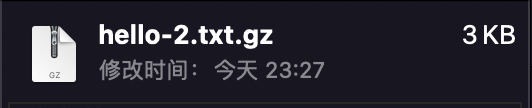
我们完成了 14KB -> 3KB 的压缩过程!是不是很有意思?不过还是那句话,有没有可能更小?当然可以!
content-encoding 响应头一般是服务器针对返回的资源响应编码格式的设置信息,常见的值有以下三种:
gzip所有浏览器都支持的通用压缩格式brotli比gzip压缩性能更好,压缩率更小的一个新的压缩格式,老版本浏览器不支持deflate出于某些原因,使用不是很广泛,后有基于该算法的zlib压缩格式,不过也使用度不高
浏览器支持的压缩格式不只是这些,不过我们列举出的是较为常用的,我们尝试使用一下这三种压缩格式:
const firstPrize = compressHello()
fs.writeFileSync('./hello-2.txt.gz', zlib.gzipSync(firstPrize))
fs.writeFileSync('./hello-2.txt.def', zlib.deflateSync(firstPrize))
fs.writeFileSync('./hello-2.txt.br', zlib.brotliCompressSync(firstPrize))
2
3
4
我们可以看到, deflate 和 gzip 的压缩率不相上下,令人惊喜的是, brotli 的压缩竟然达到了惊人的 1KB ! 这不就是我们想要的吗?

还可能更小吗?哈哈哈哈,当然,如果不考虑 HTTP 支持,我们完全可以使用如 7-zip 等压缩率更低的压缩算法去完成压缩,然后使用客户端做手动解压。不过点到为止,更重要的工作我们还没有做!
在这之前,我们需要先了解一下解压过程,如果解压后反而数据丢失,那就得不偿失了!
// 执行解压操作
const brFile = fs.readFileSync('./hello-2.txt.br')
const gzipFile = fs.readFileSync('./hello-2.txt.gz')
const deflateFile = fs.readFileSync('./hello-2.txt.def')
const brFileStr = zlib.brotliDecompressSync(brFile).toString()
const gzipFileStr = zlib.gunzipSync(gzipFile).toString()
const deflateFileStr = zlib.inflateSync(deflateFile).toString()
console.log(brFileStr)
console.log(gzipFileStr)
console.log(deflateFileStr)
console.log(brFileStr === gzipFileStr, brFileStr === deflateFileStr) // true, true
2
3
4
5
6
7
8
9
10
11
12
13
14
如上,我们知晓尽管压缩算法的效果很惊人,但是其解压后的数据依然是无损的!
# 完整的数据
让我们构建出完整的 17721088 注数据测试一下完整的压缩算法的能力如何?这里我们使用 brotli 和 gzip 算法分别进行压缩测试!
首先,应该修改我们生成数据的函数,如下:
function generateAll() {
const arrRed = Array.from({ length: 33 }, (_, index) => (index + 1).toString().padStart(2, '0'))
const arrRedResult = generateCombinations(arrRed, 6, Number.MAX_VALUE)
const result = []
arrRedResult.forEach(line => {
for (let i = 1; i <= 16; i++) {
result.push(line.join('') + i.toString().padStart(2, '0'))
}
})
return result
}
console.log(generateAll().length) // 17721088
2
3
4
5
6
7
8
9
10
11
12
13
14
15
接下来我们要经过初步压缩并将其写入文件中:
function compressAll() {
const letters = 'abcdefghijklmnopqrstuvwxyzABCDEFG'
const allStr = generateAll().join('')
let resultStr = ''
for (let i = 0; i < allStr.length; i += 2) {
const number = allStr[i] + allStr[i+1]
resultStr += letters[parseInt(number) - 1]
}
return resultStr
}
const firstPrize = compressAll()
fs.writeFileSync('./all-ball.txt', firstPrize)
2
3
4
5
6
7
8
9
10
11
12
13
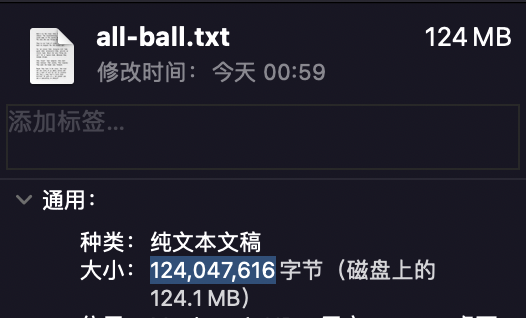
正如我们预料的,经过初步压缩之后,文件大小达到了大约 118MB,但是其实际占用 124MB,是属于计算机存储的范畴,我们现在不在本篇文章中讨论,感兴趣的同学可以自己查一查,根据字节数计算,其大小为:
const totalSize = 124047616 / 1024 / 1024 // 118.30102539 MB
目前来看是符合预期的,我们来看看两个压缩算法的真本事!
const firstPrize = compressAll()
fs.writeFileSync('./all-ball.txt.gz', zlib.gzipSync(firstPrize))
fs.writeFileSync('./all-ball.txt.br', zlib.brotliCompressSync(firstPrize))
2
3

其实是很震惊的一件事情,尽管我对 brotli 的期待足够高,也不会想到他能压缩到仅仅 4M 大小,不过对于我们来说,这是一件幸事,对于之后的分发操作有巨大的优势!
# 随机来两注
从彩票站购买彩票的时候,随机来两注的行为是非常常见的,但是当你尝试随机号码的时候,会发生什么呢?
我们先从彩票数据的分发讲起,首先彩票数据的分发安全性和稳定性的设计肯定是毋庸置疑的,但是这不是我们目前需要考虑的问题,目前我们应该解决的是,如果才能更低程度的控制成本!
假设设计这套系统的人是你,如果控制随机号码的中奖率?我的答案是,从已有的号码池里面进行选择!
如果让每个彩票站获取到其对应的号码池,答:数据分发!如果采用数据分发的模式的话,需要考虑的问题如下:
- 什么时候进行分发
- 数据回源如何做
- 如何避免所有数据被劫持
- 数据交给彩票站的策略
据 2021 年公开信息,彩票站的数量已经达到 20 万家(未查证,无参考价值),我们假设目前的彩票站数量为 30 万家!
# 什么时候进行分发
我们知道的是,彩票的购买截止时间是在晚上八点,开奖时间是在晚上的九点十五,在晚上八点之后,我们只能购买到下一期的彩票,那么这个节点应该从晚上的八点开始,计划是这样子的:
- 从目前已有的彩票库里面,按照号码出现几率从高到低排列
- 挑选出前 50 万注分发给 30 万彩票站,这个时间彩票站的数据都是统一的
- 每个小时同步一次数据,同步的是其他彩票站 "特意挑选的数据"
50 万注的数据量有多大?试试看:
function getFirstSend() {
const letters = 'abcdefghijklmnopqrstuvwxyzABCDEFG'
const doubleColorBallStr = getDoubleColorBall(500000).join('')
let resultStr = ''
for (let i = 0; i < doubleColorBallStr.length; i+=2) {
const number = doubleColorBallStr[i] + doubleColorBallStr[i+1]
resultStr += letters[parseInt(number) - 1]
}
return resultStr
}
const firstPrize = getFirstSend()
fs.writeFileSync('./first-send.txt.br', zlib.brotliCompressSync(firstPrize))
2
3
4
5
6
7
8
9
10
11
12
13

仅一张图片的大小,获取这些数据解压同步到彩票机时间不足 1s!
解压示例如下:
function decodeData(brFile) {
const result = []
const content = zlib.brotliDecompressSync(brFile)
// 按照七位每注的结构拆分
for (let i = 0; i < content.length; i += 7) {
result.push(content.slice(i, i + 8))
}
return result
}
const firstSend = fs.readFileSync('./first-send.txt.br')
const firstDataList = decodeData(firstSend)
console.log(firstDataList.length) // 500000
2
3
4
5
6
7
8
9
10
11
12
13
如何将获取到的字符形式的彩票转换为数字,如 abcdefga 转换为 ['01', '02', '03', '04', '05', '06, '01'] :
function letterToCode(letterStr) {
const result = []
const letters = 'abcdefghijklmnopqrstuvwxyzABCDEFG'
for (let i = 0; i < letterStr.length; i++) {
result.push((letters.indexOf(letterStr[i]) + 1).toString().padStart(2, '0'))
}
return result
}
2
3
4
5
6
7
8
至于分发?我们可以参考一下市面上已有的一些概念做一下对比,下面是笼统的一个网络服务器的 TPS 预估值,也就是说彩票服务器在 1 秒内可以处理的最大请求数:
- 低性能:TPS 在 50 以下,适用于低流量的应用场景,例如个人博客、小型企业网站等。
- 中性能:TPS 在 50~500 之间,适用于一般的网站和应用场景,例如中小型电商网站、社交网络等。
- 高性能:TPS 在 500~5000 之间,适用于高流量的网站和应用场景,例如大型电商网站、游戏网站等。
- 超高性能:TPS 在 5000 以上,适用于超高流量的网站和应用场景,例如互联网巨头的网站、在线游戏等。
按照这种模式的话,50 万彩票站的数据同步在 100 秒内就可以完成,当然,诸位,这里是单机模式,如果做一个彩票服务的话,单机肯定是不可能的,想要提高 TPS,那就做服务器集群,如果有 100 台服务器集群的话,处理这些请求仅仅需要 1 秒!(任性吗?有钱当然可以任性!)(这些数据的得出都是基于理论,不提供参考价值)
# 数据回源如何做
非常简单!我们需要获取的数据是哪一些呢?没有经过随机算法,直接被购买的彩票数据!也就是我们经常听到的 "守号" 的那些老彩民!
同样,根据媒体查询得知(不做参考),彩票站的客流量是每小时 1 至 10 人,经营时间,早上九点至晚上九点,最大客流量预计为 100 人每天!
那么所有彩票站的总体客流量在 100 * 500000 = 50000000,大约为五千万人次,大约有 50% 是属于 "守号" 人,这里面可能还需要排除掉彩票站中已知的号码,不过在这里我们先不处理,先做全部的预估,那么
服务器需要承载的最大 TPS 为:
// 服务器集群数量
const machineCount = 100
// 总访问量,50%中的号码才会上报
const totalVisit = 50000000 * 0.5 // 25000000
// 总的时间,因为我们计算的是 10个小时的时间,所以应该计算的总秒数为 36000 秒!
const totalSeconds = 10 * 60 * 60
console.log(totalVisit / totalSeconds / machineCount) // 6.944444444444445
2
3
4
5
6
7
8
TPS 仅为 7!!这还是没有排除掉已经知悉的号码的情况,具体的上报逻辑,参考下图:
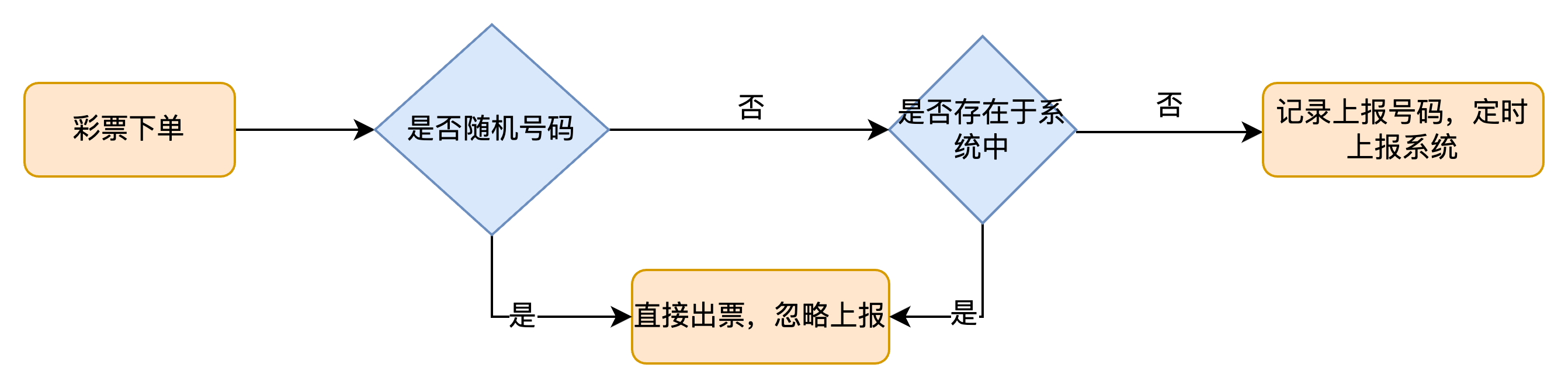
# 数据交给彩票站的策略 (避免数据被劫持)
所有的彩票数据当然不能全部都交给彩票站,我们需要对所有的数据做一个分层,其他彩票站 "特意挑选的数据" 就是我们要分层分发的数据!这样子也就能解决 "如何避免所有数据被劫持" 的问题!
那么我们如何对数据进行分层呢?
简而言之,就是我们将陕西西安彩票站的购票信息同步给山西太原,将上海市购票信息同步给江苏苏州!当然这里面需要考虑的点非常多,不仅仅是两地数据的交换,逻辑也比较复杂,通常需要考虑的点是:
- 数据同步难度,跨地区同步对服务器压力巨大,如华南向华北同步
- 数据相似程度,两地的数据如果历史以来相似度区别很大,反而不能达到覆盖的目的,因为我们最终是想要这注号码被购买更多次
- 数据同步时差,如新疆等地,鉴于网络问题,比其他地要慢很多的情况,这样就会漏号,那么就应该把这些地方的数据同步到更繁华的区域,如上海市,但是这一点看似是和第一二点相悖的
就说这么多,说的多了其实我也不懂。或者说还没想出来,如果有这方面比较厉害的大佬,可以提供思路!我们先看看随机的号码结果如何:
我们来尝试随机获取你需要的两注:
function random(count) {
let result = []
for (let i = 0; i < count; i++) {
const index = Math.floor(Math.random() * firstDataList.length)
console.log(firstDataList[index])
result.push(letterToCode(firstDataList[index]))
}
return result
}
console.log(random(2))
2
3
4
5
6
7
8
9
10
11

OK,你觉得可以中奖吗?哈哈哈,还是有可能的,继续往下看吧!
# 特意挑的两注
我是一个典型的 "守号" 人,每天都拿着自己算出来的几注号码,去购买彩票,那么我可以中奖吗?(目前没中)
根据上面的描述,我们应该知道,"守号" 人购买的号码需要判断系统是否存在数据,如果存在的话,就不会触发上报,如果数据不存在,则会上报系统,由系统将当前号码分发给相邻市或数据近似的城市,预期当前号码可以被更多的人所购买,一注号码如果被购买的越多,其中奖的概率也就越低!
不过特意挑选是要比随机挑选的中奖概率要大,但是也大不到哪里去。
# 我要一等奖
彩票的一等奖是基于统计的,即使彩票中心存在空号,也需要考虑空号所产生的二等奖至六等奖的数量,这是一个非常庞大的数据量,也是需要计算非常多的时间的,那么我们如何模拟呢?
我们取 50 万注彩票,模拟一下这些彩票被购买的情况,可能会产生空号,可能会重复购买,或者购买多注等,尝试一下计算出我们需要付出的总金额!
彩票中中奖规则是这样子的,浮动奖项我们暂时不考虑,给一等奖和二等奖都赋予固定的金额:
- 6 + 1 一等奖 奖金 500 万
- 6 + 0 二等奖 奖金 30 万
- 5 + 1 三等奖 奖金 3000 元
- 5 + 0 或 4 + 1 四等奖 奖金 200 元
- 4 + 0 或 3 + 1 五等奖 奖金 10 元
- 2 + 1 或 1 + 1 或 0 + 1 都是 六等奖 奖金 5 元
根据这个规则,我们可以先写出对奖的函数:
/**
* @param {String[]} target ['01', '02', '03', '04', '05', '06', '07']
* @param {String[]} origin ['01', '02', '03', '04', '05', '06', '07']
* @returns {Number} 返回当前彩票的中奖金额
*/
function compareToMoney(target, origin) {
let money = 0
let rightMatched = target[6] === origin[6]
// 求左边六位的交集数量
let leftMatchCount = target.slice(0, 6).filter(
c => origin.slice(0,6).includes(c)
).length
if (leftMatchCount === 6 && rightMatched) {
money += 5000000
} else if (leftMatchCount === 6 && !rightMatched) {
money += 300000
} else if (leftMatchCount === 5 && rightMatched) {
money += 3000
} else if (leftMatchCount === 5 && !rightMatched) {
money += 200
} else if (leftMatchCount === 4 && rightMatched) {
money += 200
} else if (leftMatchCount === 4 && !rightMatched) {
money += 10
} else if (leftMatchCount === 3 && rightMatched) {
money += 10
} else if (leftMatchCount === 2 && rightMatched) {
money += 5
} else if (leftMatchCount === 1 && rightMatched) {
money += 5
} else if (rightMatched) {
money += 5
}
return money
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
那么,应该如何得到利益最大化,步骤应该是这样子:
- 随机生成一组中奖号码
- 对于每个购买的数字,检查是否与中奖号码匹配,并计算它的奖金金额
- 对于所有购买的数字的奖金金额进行求和
- 重复这个过程,直到找到最优的中奖号码
随机这个中奖号码非常重要,他决定着我们计算出整体数据的速度,所以我们按照下面的步骤进行获取:
- 将所有的号码按照购买数量进行排序(其实这里真实的场景应该联合考虑中奖号码的分布趋势才更精确)
- 从空号开始查询,依次进行计算
先模拟出我们的购买数据:
function getRandomCode(count = 500000) {
const arrRed = Array.from({ length: 33 }, (_, index) => (index + 1).toString().padStart(2, '0'))
// generateCombinations 是我们上面定义过的函数
const arrRedResult = generateCombinations(arrRed, 6, count)
const result = []
let blue = 1
arrRedResult.forEach(line => {
result.push([...line, (blue++).toString().padStart(2, '0')])
if (blue > 16) {
blue = 1
}
})
return result
}
function randomPurchase() {
const codes = getRandomCode()
const result = []
for (let code of codes) {
let count = Math.floor(Math.random() * 50)
result.push({
code,
count,
})
}
return result
}
console.log(randomPurchase())
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
我们将得到类似于下面的数据结构,这对于统计来说较为方便:
[
{
code: [
'01', '02',
'03', '04',
'05', '10',
'05'
],
count: 17
},
{
code: [
'01', '02',
'03', '04',
'05', '11',
'06'
],
count: 4
}
]
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
接下来,就是很简单的统计了,逻辑很简单,但对于数据量极为庞大的彩票来说,需要的时间!
// 空号在前,购买数量越多越靠后
const purchaseList = randomPurchase().sort((a, b) => a.count - b.count)
const bonusPool = []
for (let i = 0; i < purchaseList.length; i++) {
// 假设这就是一等奖,那么就需要计算其价值
const firstPrize = purchaseList[0]
let totalMoney = 0
for (let j = 0; j < purchaseList.length; j++) {
// 与一等奖进行对比,对比规则是参照彩票中奖规则
const money = compareToMoney(purchaseList[j].code, firstPrize.code) * purchaseList[j].count
totalMoney += money
}
bonusPool.push({
code: firstPrize.code,
totalMoney,
})
}
const result = bonusPool.sort((a, b) => a.totalMoney - b.totalMoney)
// 至于怎么挑,那就随心所欲了
console.log(result[0].code, result[0].totalMoney)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
至于最后的一等奖怎么挑,那就随心所欲了,不过上面的算法在我的 M1 芯片计算需要的时间也将近 10 分钟,如果有更强大的机器,更厉害的算法,这个时长同样可以缩短,不展开了,累了,就这样吧!
# 黄粱一梦
终归是黄粱一梦,最终还是要回归生活,好好工作!不过谁知道呢,等会再买一注如何?
彩票系统纯属臆测,不可能有雷同!
# 结语
我是泰罗凹凸曼,M78 星云最爱写代码的,我们下一篇再会!
去探索,不知道的东西还多着呢!